Box, George E. P. (1976) Science and Statistics, Journal of the American Statistical Association,  71(356): 791-799’dan Türkçeleştirildi.

Özet 
1. Giriş
2. Bilimsel Yöntemin Nitelikleri
2.1 Kuram ve Uygulama Arasındaki İterasyon
2.2 Esneklik
2.3 Tutumluluk
2.4 Önemli Olanı Ayırdetme
2.5 Matematiğin Bilimdeki Yeri
3. Fisher – Bir Bilimci
3.1 Rothamsted
3.2 Bebeği Tartma
3.3 Hanımefendiyi Bul
3.4 Toprak Bakterilerinden Doğrusal Olmayan Tasarıma
3.5 Pamuktan Uç Değerlere
3.6 Gübreden Ortogonal Polinomlara ve Artık Çözümlemeye
3.7 Yaban Otları ve Eğitim Yasaları
3.8 Yağış ve Buğday Veriminden Dağıtılmış Gecikmelere
3.9 Gübre ve Patateslerden Varyans Analizine
3.10 Fareler, Kaplanlar ve Rassallaştırma
3.11 Gübre Tırmıklamadan Grup Kuramına
3.12 Yeni Yöntemlerin Evrimi
3.13 Uygulayıcıları İkna Etmek
3.14 İstatistikçiler için Yeni Bir Miras
4. Açık Döngünün Tehlikeleri
4.1 Kitap-ahçılığı ve Matematikçilik
4.2 Meydan Okumaya Karşılık Verme
4.3 İstatistikçilerin Eğitimi
5. Sonuç
Başvurular

Bilimsel yöntemin nitelikleri, özellikle uygulamanın kuramı ve kuramın uygulamayı izlediği yönlendirilmiş bir iterasyon olarak algılanması tartışılıyor. Hızlı ilerleme, bu tür etkileşimlerden yarar sağlamak için yeterli esneklik, tutumlu ancak etkin model tasarlama, model yetersizlikleri konusunda yerinde kaygı duyma ve matematiği ustaca ama kararında kullanma yeteneği gerektirir. Sir Ronald Fisher tarafından Rothamsted Deney İstasyonu’nda istatistik yöntemlerinin geliştirilmesi, bu temaların işlenmesinde kullanılıyor.⇑

1952’de, R.A.Fisher’i Chicago Üniversitesi’nde Onursal Bilim Doktoru derecesi için takdim ederken, W.Allen Wallis onu şu sözlerle tanıtıyordu:

Aralarında  ziraat, antropoloji, astronomi, bakteriyoloji, botanik, iktisat, ormancılık, meteoroloji, psikoloji, halk sağlığı, ve -hepsinin başında- önderlerinden biri olduğu bilinen genetik gibi pek çok bilim alanında katkılarda bulunmuştur. Bu bilimsel araştırmalar ve matematikteki ustalığının  ötesinde, deneysel verilerin yorumlanması için sistematik ilkeler geliştirmiş ve bir deneysel tasarım bilimi kurmuştur. Onun attığı bu temeller üzerinde, insanoğlunun deney ve gözlem yoluyla doğayı  kavramaya giriştiğinde kullandığı bir istatistik teknikler yapısı yükselmiştir.

Fisher, yayınlanmış makalelerinin yarıdan çoğunun istatistik ve matematik dışındaki konularda olduğuna bakılırsa, kendisinin de yeğleyeceği çok yerinde bir ünvanla –bir istatistikçi olarak değil bir bilimci olarak tanıtılmıştı. Dolayısı ile yaklaşımım önce, bir istatistikçi olarak onun hayranlık verici dehası, özgünlüğü, girişimciliği, ve üretkenliğinde, bir bilimci olmasının oynadığı rolü göstermek ve sonra bunun bizim için şimdi ne mesaj taşıdığını gözler önüne sermek olacaktır..⇑

Bilimsel öğrenme sürecine ilişkin düşünce mirasımız, Aristotle, Galen, Grossteste, Occam’lı William ve Bacon gibi gerçek bilimin niteliklerini vurgulayan ve tuzaklardan haberdar yazarlardan gelir..⇑

Önemli bir düşünce, bilimin yalnızca bir yandan ne kuramsal kurguyla, ne de öbür yandan pratik gerçeklerin başıboş birikimi ile değil, Şekil A(1) de gösterildiği gibi, daha çok kuramla uygulama arasında yönlendirilmiş bir iterasyonla bilgiye ulaşılan bir araç olduğudur.

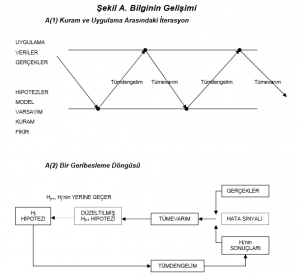Eldeki gerçek geçici bir kurama yol açar. Bu geçici kuramdan yapılan tümdengelimlerin bilinen ya da özellikle elde edilmiş belirli gerçeklerle uyumlu olmadığı görülebilir. O zaman bu uyumsuzluklar, düzeltilmiş ya da bazı durumlarda farklı bir kuramı savunmayı gerektirir. Bu kez düzeltilmiş kuramdan yapılan tümdengelimler gerçekle çelişki içinde olabilir ya da olmayabilir ve bu böylece sürer gider. Gerçekte bu ana iterasyona bir çok eşanlı alt iterasyonlar eşlik eder(örneğin, [1,2]’ye bknz.)..⇑

Bu nedenle, etkin bilimsel iterasyonun engellenmemiş geri besleme gerektirdiği açıktır. Şekil A(2) de iterasyon düzeni bir geri besleme döngüsü olarak gösterilmiştir. Herhangi bir geribesleme döngüsünde bizi bilgilendirecek olan tabii ki hata sinyali- örneğin, geçici kurama göre olacak olanla gerçekte olan arasındaki farktır. İyi bilimci böyle hataları-özellikle de kendi hatalarını- arama, bulma, ve onlardan yararlanma esneklik ve cesaretine sahip olmalıdır. Bacon’ın benzetmesini kullanacak olursak özellikle, Pygmalion gibi kendi yarattığı modele aşık olmamalıdır..⇑

2.3 Tutumluluk

Tüm modeller yanlış olduğundan bilimci çok ince ayrıntılama ile “doğru” bir modele ulaşamaz. Tersine, Occam’lı William’ı izleyerek, doğasal olgunun tutumlu bir betimlemesini amaçlamalıdır. Yalın ama olguyu canlandıran modeller tasarlama yeteneği nasıl büyük bilimcinin damgası ise, aşırı ayrıntılama ve aşırı parametrelendirme de genellikle yetersizliğin işaretidir..⇑

Tüm modeller yanlış olduğuna göre, bilimci önemli olan yanlışa karşı uyanık olmalıdır. Kaplanlar çevremizde dolanırken farelerle uğraşmak anlamsızdır..⇑

Salt matematik “A’nın doğru olması, B’nin de doğru olmasını gerektirir mi?” türünden önermelerle ilgilenir. Bu koşullu bir ifade olduğundan , ne A’nın ne de onun sonucu B’nin gerçek yaşamda geçerli olup olmadığı konusunda yapacağı bir şey yoktur. Salt matematikçinin bu çerçevede pratik sorunlarla ilgilenmesine gerek yoktur, ve belki de hiç ilgilenmemelidir.

Matematiği fizik ve istatistik gibi konulara uygularken gerçek dünya hakkında hatalı olduğunu bildiğimiz ancak yine de yararlı olabileceğine inandığımız geçici sayıltılar yaparız. Fizikçi bilir ki parçacıklar kütleye sahiptir, ancak gerçekte olanı yaklaşıklayarak, kütlelerinin olmadığı sayıltısından yine de belirli sonuçlar çıkarabilir. Aynı biçimde, istatistikçi de, örneğin doğada ne normal dağılım ne de düzgün bir doğru bulunmadığını bilir, yine de gerçekte olmayan normallik ve doğrusallık sayıltıları ile gerçek dünyada gözlenenlere yeterince yakın olan sonuçları genellikle elde edebilir.

Buradan, mantıksal sonuçların özenle türetilmesinin istatistikçi için büyük önemine karşılık, zorunlu olarak öncül ve buradan ulaşılan sonuç bilgisi içinde kalan böyle türetmelerin doğal gerçeği betimleyemecekleri çıkarılır. Bu yüzden geliştirdiğimiz herhangi bir istatistiksel tekniği kullanmadıkça onun yararlı olduğunu bilemeyiz. Bilimde ve özellikle istatistik bilimindeki büyük ilerlemeler bu nedenle, genellikle, kuram-uygulama iterasyonunun sonucu olarak ortaya çıkar.

Deney tasarım kuramına yeni bir katkıda bulunmayı uman bir araştırmacının kendisi gerçek deneylerin tasarımı ile uğraşmalıdır. Karar kuramında devrime yolaçmayı bekleyen bir araştırıcı, önemli kararların alınmasını gözlemlemeli ve böyle kararların alınmasına katılmalıdır. Uygun biçimde seçilmiş bir ortam, böyle bir araştırıcıya incelenmeye değer yeni kuramlar ve modeller sağlıyabilir. O zaman ustaca kullanılan matematik ^* , geçici varsayımların mantıksal sonuçlarını türetmesine ve stratejik biçimde seçilmiş çevresi de bu sonuçları pratik gerçeklerle karşılaştırmasına olanak verecektir. Bu yolla sonunda amacına ulaşabileceği bir iterasyonu başlatabilir. Gerçekle zorunlu bir ilişiği bulunmayan matematiksel çözümlerin eniyi olduğunu söyleyerek deney tasarımı ve karar sözcüklerini yeniden tanımlamak da bir seçenektir..⇑

---

^* Araştırmacının salt matematiksel zekası, gerçek sorunlarla uğraşması durumunda daha az değil ama daha çok sınanacak gibidir.

Aklımızdaki bu düşüncelerle, onun Rothamsted Deney İstasyonu’nda bulunduğu sıralarda yaşanan bazı olayları aktararak, Fisher’in nasıl bir bilimci olduğunu görelim.

Fisher, 1919 da, İngiltere ve hatta o zamanlar dünyadaki en gözde istatistik laboratuarında Karl Pearson’un yönetiminde çalışmanın güven ve saygınlığını geri çevirmişti. Bunun yerine, kent dışındaki küçük bir tarımsal araştırma istasyonunun tek istatistikçisi olarak geçici bir iş buldu. 29 yaşındaydı ve o zamana kadar giriştiği her iki işde de (öğretmenlik ve aktüerlik) başarısızlığının farkında olduğunu sonradan söylemiştir.

O zaman Rothamsted’in Yöneticisi olan Sir John Russell, sonradan şöyle anımsıyor [17, s.326]:

…1919 da onu ilk gördüğümde bir işten yeni ayrılmıştı. Herhangi bir karara varmadan önce, matematiğe yatkınlığını öğrenmek üzere Caius kolejindeki öğretmenine yazdım…Gelen yanıt, “iplere sarılsa” birinci sınıf bir matematikçi olabilecek iken, bunu yapmayacağı yolundaydı. Aradığımız adam tipine benzer gibiydi. …Yalnızca 200₤’dum vardı ve bu miktarın yeterli olduğunu düşündüğü sürece kalabileceğini önerdim…Evimdeki çayda bana haftalık rapor verirdi…Çok yetenekli bir kişiden daha fazlası, hatta bir dahi olduğunu anlamam çok kısa bir zamanımı aldı.

Bir yılın sonunda, evli ve iki çocuklu olan Fisher, 200₤’un iki katını tüketmiş, ancak bu arada da sürekli bir yer edinmişti..⇑

Kuram-uygulama iterasyonunun işlemesi için, iterasyon gibi zihnen iki yönlü olmalı; bir yandan yaşadığımız dünyanın pratik gerçeği ve verilerinden ulaşılacak geçici modeller, kuramlar, ve muhtemel anlamlara eğilirken, diğer yandan gerçek dünyaya uygulanabilir geçici kuramlar, modeller, ve hipotezlerden çıkarılabilecek önermelere de aynı ölçüde eğilmelidir.

Fisher’in pratik sorunlara büyük ilgisi vardı. Örneğin, Araştırma İşcileri İçin İstatistiksel Yöntemler kitabının asıl konusuna 2.Bölümü’nde, verilerin farklı gösterim yollarını tartışarak başlar. İlk örneği şöyledir [12, s.25]: “ Şekil 1 bir bebeğin doğumdan itibaren eşit arlıklarla en yakın ons olarak ölçülmüş büyümesini göstermektedir.” Bunun belirli bir bebek olduğunu söylememektedir. Yakın bir zamanda, sonuçların özenle grafikleştirildiği, dokuz çocuğunun her birinin doğumundan başlayarak ağırlıklarını Fisher’in kendi eliyle kaydettiği Fisher aile kayıtlarını görme şansım oldu. Karşılaştırma, bu çocuğun, kitabın ilk baskısının yapıldığı 1923’ten kısa bir süre önce doğan ikinci oğlu Harry Leonard olduğunu gösteriyor. “Öne sürülen herhangi bir artış yasası ile kabaca uyum içinde olduğunu” gösterecek biçimde verilerin en iyi nasıl gösterileceğini tartışmaya devam ederek, bilimsel iterasyonun sonraki adımına ipucu verilir..⇑

3.3 Hanımefendiyi Bul

Tümevarımcı aklının değirmeninde öğütülecek tahıl olan Fisher’in günlük gerçek deneyiminin uzandığı olağanüstü uç, Fisher’in Deneylerin Tasarımı kitabının II. Bölümünün ünlü açılış satırlarında biraz daha gözler önüne serilir [11, s.11]: “ Bir hanımefendi, fincandaki çayı tadarak, fincandaki karışıma önce sütün mü, yoksa çayın mı eklendiğini ayırt edebileceğini söylemektedir. Bu iddianın sınanabilmesine olanak verecek bir deneyin tasarım sorununu ele alacağız.” Fisher bu örneği, iyi bir istatistiksel tasarımın temel ilkelerini açıklama ve göstermede kullanmaya başlayarak devam eder.

Elbette, gerçek bir hanımefendi vardı. Bu olay, kitap yazılmadan çok yıllar önce ve Fisher’in Rothamsted’e gelişinden hemen sonra yaşandı. Bu hanımefendi, Fisher’in ikram ettiği çay fincanını, içine önce çay koyduğu için geri çeviren, yosunbilimci Dr.Muriel Bristol’du. Bunun fark etmeyeceğini belirten Fisher’e hanımefendinin yanıtı, “Elbette fark etti.” olur. Yanıbaşlarındaki sonradan kocası olan William Roach, “Onu sınayalım” der, sınarlar, ve hemen hemen her seçimi doğru yaptığını görürler. Burada o, kitaptaki bir tek yanlış seçim yapan hanımefendi gibidir..⇑

Çay semaveri iterasyon için büyük bir kolaylaştırıcıydı.Orada, her öğleden sonra, bilimciler ve konuklarla sohbet ediyor ve çarpıcı sonuçlara yol açan biçimde onların sorunlarına dalıyordu. Fisher’le hemen hemen aynı zamanda Rothamsted’e gelen ve onunla çok yakın bir dost olan bilimci, bakteriolog Gerard Thornton’du. Bakteri sayımı için zaman alıcı sulandırma yöntemlerinin geliştirilmesine Fisher’in ilgisini çeken ilk o oldu. Bu, Cochran [4] tarafından bahsedilen, 1922 deki Fisher’in doğrusal olmayan tasarım üzerine öncü çalışması ile sonuçlandı..⇑

3.5 Pamuktan Uç Değerlere

Rothamsted’in ilk ziyaretçilerinden biri Pamuk Araştırma Enstitüsü’nden L.H.C.Tippett’ti. Pamuk ipliğinin dayanıklılığı onun için pratik önemi büyük bir ilgi konusuydu. Bir tutam pamuğun kopma kuvveti en zayıf bağın kuvveti olduğundan, şimdi uç değer olarak adlandırdığımız sorunla yüz yüzeydi. Tippett önce Karl Pearson’la çalışmış ve momentler yöntemini kullanarak dağılımı yakınsamıştı. Fisher’le işbirliğinde soruna daha farklı yaklaşıldı. Yazarlar, “ limitsel dağılımın, böyle bir dağılımdan alınan n çaplı bir örneğin uç değerinin kendisinin de aynı dağılımlı olacak biçimde olması gerektiğine” işaret ederler [14, s.180]. Bu basit ama olağanüstü kavrayış, temel limitsel biçimleri çözüm olarak veren fonksiyonel bir denkleme götürür. Bu konuda sonraki çalışmaların hemen tümü bu biçimlerden çıkmıştır. Kuramın, baraj tasarımı ve parçaların güvenirliği gibi çok farklı alanlarda uygulamaları bulunmaktadır.

Fisher’in diğer buluşlarının bir çoğu gibi, bu da şimdi ayrı bir çalışma alanı olarak görülmektedir.

Biraz daha ileri düzeyde örnek için, Fisher’in 1919’la 1927 arasında regresyon çözümlemesi ile başlayıp bugün bile istatistiksel olarak planlanmış bir çok deneyin temeli olan tam ve kusursuz bir deney tasarım kuramı ile sonuçlanan Rothamsted’de yaptığı çalışmayı kullanacağım. Bu çalışma, I, II, III ² ,IV, ve VI numaralı ve genel başlığı “Ürün Değişmesi Üzerine Çalışmalar” olan bir dizi makale olarak yayınlandı [7, 13, 8, 5, 6]..⇑

Broadbalk’taki 13 parsel buğday tarlası, 1919’ a gelindiğinde, 67 yıl boyunca aynı biçimde onüç farklı gübreleme işlemi görmüştü. “Ürün Değişmesi Üzerine Çalışmalar I” [7]’de Fisher, Broadbalk verilerinin çözümlenmesiyle ulaşılan ve oniki sayfa tutan, onüç farklı gübrelemenin sonuçlarını bir ustaya yakışır tartışma ile başlar. Özel olarak, gerçekten düz gübre gibi başka bir şeyin olmadığı sonucuna varır. Uzun yıllar boyunca önemli bir azalış göstermeden yüksek bir verim vermektedir. Sonra, gübreden çözümlemesinin nereden geldiğini gösteren matematiğe ansızın kayar. Sonraki birkaç sayfada, ortogonal polinomları, eşit aralıklı verilerden hesaplama formüllerini sunar, katsayıların dağılım özelliklerini elde eder, ve anlamlılıklarının nasıl yargılanabileceğini gösterir. Adını söylemeksizin, yıllık verimlere beşinci dereceden polinom uyarlarken kullandığı uygun varyans çözümlemesini sunar. Hepsinden ilginci, uyarlanmış her hangi bir r dereceli polinomun \(y-\hat y\) artıklarının özelliklerini tartışır ve şimdi kimilerinin veri çözümleyici dedikleri bir kimlikte onu görmemize izin verir.

Araştırma sürecinde bir alt iterasyon olan veri çözümleme burada gösterilmiştir.

Tümevarımsal aşamada, çözümleyici modelin destekleyicisidir. Modelin gerçeği yansıttığı varsayımıyla, verilerin çözümlenmesi için eniyi istatistiksel yöntemi seçer. Ancak çözümleme tamamlandığında, rolünü destekleyicilikten eleştiriciliğe ³ çevirmelidir.Şimdi modelin kuşkulanılan ya da kuşkulanılmayan, bir veya daha fazla ciddi biçimde hatalı olabileceği karşı varsayımı ile, çeşitli artık çözümleme biçimlerini içeren uygun tanısal sağlamaları uygular.

Uygulanan polinomların verdiği artıkların çözümlenmesini yürütmek için Fisher,

i. \((1 – (r + 1)/n){\sigma ^2}\) biçiminde \(V(y – \hat y)\)’nin ortalama değerini,

ii. 67 gözlemin her biri için \({y_j} – {\hat y_j}\) artığının varyansını,

iii.\({\sigma ^2} = V({y_j}) = V({y_j} – {\hat y_j}) + V({\hat y_j}){\rm{ }},{\rm{ }}j = 1,2,…,n{\rm{ }}\) özdeşliğini,

iv. her hangi bir dereceden polinom artıklarının otokorelasyonları için yaklaşık bir formül

elde eder.

\(V(\hat y)\)’nin ortalama değeri, (i) ve (ii)’den \({\sigma ^2}(r + 1)/n\) olarak bulunur. Böylece Fisher, yalnızca beşinci dereceden polinomları kullanmasını haklı çıkaran ve tutumluluğun değerini gösteren bir biçimde, eğer
\(\hat y\) için küçük bir varyans istiyorsak \(r \)yi küçük tutmamız gerektiğini söyler. Fisher, her artığın \(V({y_j} – {\hat y_j})\) varyanslarını zaman sıraları \(j\)’ye karşı çizer. Grafik yukardan aşağı bakıldığında, ilişki (iii)’ten dolayı \(V(\hat y_j)\)’nin de bir grafiğidir. Bunu kullanarak ölçek uçlarında \(V({y_j} – {\hat y_j})\)’nin aldatıcı azalışı ve buna karşılık \(V(\hat y_j)\)’deki artışa işaret ederek, “uç terimlerin bu kadar çok etkileniyor olması, polinomiyal biçimin bir zayıflığıdır” der[7, s.123].

Sonuç olarak, hem yüksek ve hem de alçak derecelendirmenin önlenlenmesi gerektiğinden söz ederek, yeteri kadar yüksek dereceli bir polinomun uygulanmış olduğunu anlamak için artıkların kuramsal ve ampirik otokorelasyonlarının uyuşmasına bakar. Özel olarak, sıfır ve beşinci dereceden polinom artıklarının kuramsal ve gözlemsel otokorelasyonlarını, öncekinin yetersiz, sonrakinin yeterince uygun olduğunu göstermek için karşılaştırır. Hangi noktada uyum yeterliğine ulaşıldığına karar verme gibi güç bir soruna artıkların dizisel korelasyonunun bu uygulaması, 55 yıl sonra büyük bir canlılık ve ilgiye sahiptir..⇑

Çizdiği ürün grafiklerinin biçimleri Fisher’i hayrete düşürdü. Bunlar 13 Broadbalk parselinin hepsinde ortak biçimde anlamlı bir yavaş değişme kalıbı göstermekteydi. Özellikle aşağı yukarı 1870-1880 döneminde düşük ürüne doğru ortak bir eğilim vardı. Bu ortak kalıp hava durumundan dolayı değildi; Woburn’da deneysel buğday ürünü, tüm Herfordshire’da buğday ortalamaları, ve Rothamsted’de ki deneysel parsellerdeki arpa ve ot dizilerine uyguladığı benzer bir çözümleme böyle olmadığını gösterdi. “Buğday verimini etkileyen tüm organik faktörlerin içinde, Broadbalk’taki değişmeyi açıklamak için yalnızca yaban otlarındaki yavaş değişmenin yeterli olabileceğini” öne sürer[7, s.129].

Ancak kendini işine adayan bir bahçıvanın yapabileceği gibi, orada bulunan tüm yabani otları tarif ederek devam eder. Eski kayıtların, 1853’te alanın yaban otlardan temizlenmesinde, 211 yetişkin erkek-gün ve 714 erkek çocuk-gün harcandığına işaret eder. Özellikle, uzun ince tilki kuyruğu otu, Alopecuris agrestis’in elle ayıklanmasına muhtemelen erkek çocuklar koşuluyordu. Ancak, “1876 ve 1880 Eğitim Yasaları’nın okula devamı zorunluluğu getirdiği hatırlanabilir.” der[7, s.131]. Bize de, o zamandan sonra oluşan düşük buğday verimininin, tilki kuyruğu otunu yolan küçük erkek çocuk ellerinin şimdi toprağa değil mürekkebe bulanmış olmasından dolayı mı olduğunu düşünmek kalır..⇑

1924’te, dizinin üçüncü makalesi [8] de, Broadbalk verilerini,yağışların buğday verimi üzerindeki etkisini göstermede kullandı. Makalenin başında, yalnızca yağışın değil, en düşük ve en yüksek sıcaklık, çiğ noktası, ve parlak gün ışığı saatleri gibi diğer değişkenleri de hesaba katmış olmasının beklenmesinden çekinir görünür. Ancak, en azından her biri için ayrı ayrı son hasat verimi üzerindeki etksinin göz önüne alınmasının gerekeceğine işaret eder. Ve eğer bu kadar çok açıklayıcı değişken içerilirse, toplam değişmenin çok büyük bir oranının tek başına rastlantı ile açıklanmış gibi görülebileceğini söyler. Kimi karşıt görüşlü okuyucunun kuşkusuna karşın, doğrudan doğruya n-boyutlu geometriyi kullanarak çoklu korelasyon katsayısının dağılımını türetilmesini özetler ve sonraki sayfada R için kuyruk alanlarının kısa bir çizelgesini üretir. Sonra, şimdi adım-adım regresyon denen yöntemde seçimin yanlış yönlendirici etkilerini tartışmaya devam eder.

Fisher’in verileri şunlardı:

1. 13 Broadbalk parselinin her biri için 60 yıllık buğday hasat verimleri ⁴ ,
2. her yıl için hemen hasattan sonra başlayan altı-gün periyodlu 61gözleme toplulaştırılmış (6×61=366) bu 60 yıl için günlük yağışlar.

Tutumlu modellemenin olağanüstü bir örneği olarak, önce \(j\)’inci yıldaki buğday verimi, diyelim ki, \(w_j\)’nin

\({w_j} = c + \sum\limits_t^{61} {{a_t}{r_{jt}}} {\rm{ }}{\rm{, }}j = 1,2,…….,60.\)      (3.1)

ile gösterilebileceğini öne sürer.

Bu modelde \(a_t\), \(t\)’inci zamanda bir inçlik yağışın son hasat üzerindeki ortalama etkisini gösterir. Çağdaş deyimle, (3.1)’e sistemin “belleği”ni ifade eden bir “transfer fonksiyonu” modelidir denebilir. Daha sonraları iktisatçılar onu “dağıtılmış gecikme” modeli olarak adlandırdılar, ancak Fisher’in önceki çalışmasından ya da onun ortogonal polinomlardan yararlanarak ilerleyen ustaca yolundan haberlerinin olmadığı görülüyor.

Görüldüğü gibi (3.1) çok savurgandır. Dolayısı ile Fisher, \(r_{jt}\) yağış verilerini beşinci dereceden polinomlarla göstermeye karar verdi. Şimdi o, \(a_t\) katsayılarının aynı yolla gösterilebilecek düzgün bir eğriyi izleyeceğine dikkat çeker. Buradan,

\[{a_t} = {\alpha _0}{T_{0t}} + {\alpha _1}{T_{1t}} + ….. + {\alpha _5}{T_{5t}}{\rm{ }}{\rm{, }}{r_{jt}} = {\rho _{0j}}{T_{0t}} + {\rho _{1j}}{T_{1t}} + ….. + {\rho _{5j}}{T_{5t}}{\rm{ }}{\rm{.}}\]

Ancak, \(T_{it}\) polinomiyal foksiyonları \(\sum\nolimits_t {T_{it}^2 = 1} \) olacak biçimde seçilirse; toplamadan sonra, (3.1)

\[{w_j} = c + {\alpha _0}{\rho _{0j}} + {\alpha _1}{\rho _{1j}} + ……. + {\alpha _5}{\rho _{5j}}\]

olarak yazılabilir. Transfer fonksiyonundaki \(\alpha\)’lar \(w_j\)’nin tahmin edilen \(\rho\)’lar üzerine regresyonundan böyle elde edilebilir. Gerekli yoğun hesaplamaları yapan ve sonuçları grafikleştiren Fisher, özellikle yağışların toprak nitratlarını azaltmadaki baskın etkisine ulaştığı, farklı biçimde gübrelenmiş parseller için polinomiyal dağılımlı gecikme eğrilerinin çok yoğun bir karşılaştırma ve tartışmasını yürütür. Hesaplamaları kendisinin ve yardımcısının elle yürütmüş olması gerçeği ile, onun tutumluluğa olan bağlılığının asla azalmadığını biri hisseder. Gerçekten, onun hesaplama ve sağlamanın tutumlu yöntemlerine ilişkin tartışmasından daha fazlası da öğrenilebilir[8,s.111-3]..⇑

Bu sıralarda Fisher eski kayıtların analizinden giderek sıkılmaktadır-daha sonra bunu “gübre yığınını tırmıklamak” diye tanımlar. Yardımcısı Bayan W.A. MacKenzie ile birlikte yazdıkları “Üründeki Değişmeler Üzerine Çalışmalar II,”nin “Farklı Patates Türlerinin Gübrelemeye Tepkisi”[13] alt başlıklı bölümünde, Rothamsted’den bazı deneysel verilere el attı. Yazarlar, (kimi uzman görüşün tersine) farklı bitki türlerinin gübrelere farklı tepki göstermemesinin, ya da şimdi söylediğimiz gibi, tür ve gübre arasında etkileşim olmamasının daha uygun olacağına işaret ederler.

Rothamsted’de bir ürün ekoloğu olan Thomas Eden tarafından son zamanda, oniki patates türünün her birinin altı farklı gübre kombinasyonu ile sınandığı bir deney yürütülmüştü. Bu deney, üç kez yinelenen ve rassallaştırılmış 12 x 6 faktöriyelmiş gibi çözümlendi. (Aslında öyle değildi, ancak buna daha sonra döneceğiz.)

Sunulan varyans analizinden, “Türler ve gübreler arasında anlamlı bir etkileşim var mı?” sorusuna yanıtın Hayır! olduğu görülür. Ancak bu makaleye ilişkin dikkate değer bazı şeyler vardır:

i. Daha önce ipucu verilen varyans çözümlemesi, burada ilk defa bütünüyle görülür. Tarımsal sorunların tartışılmasından sonra makalenin ortasında, hiç duyurulmadan ve birden gelir. Tabi ki başlıkta bile bahsedilmemiştir.

ii. Tüm kareler toplamı ile işlemler arası ve içi kareler toplamları arasındaki cebirsel özdeşlik yazıldıktan sonra , “Sanki numaraları karıştırılmış ve rassal bir sırada yazılmış gibi parseller arasında fark görülmezse, iki kısımın her birinin ortalama değeri, karşılaştırıldıkları değişmedeki serbestlik derecesi sayısına orantılıdır.” ifadesi kullanılır[13, s.315]. Böylece, en baştan, Fisher’in altında yelken açacağı rassallaştırma bayrağı direğe çekilir.

iii. Gerçekte deneme şimdi bölünmüş parsel tasarımı denen biçimde yapıldığından çözümleme yanlıştır. İstatistiksel Yöntemler’in 1925’deki ilk baskısında ([12, s. 238]’e bakın) uygun düzeltme biçiminde geribesleme çabucak geldi. Aynı verilerin bir bölümünü kullanarak, Fisher orda doğru çözümlemeyi verir ve (parseller arası ve içi karşılaştırmalar için) ayrı hata varyans tahminleri kullanmanın esas olduğuna işaret eder ve birinin diğerinden gerçekten anlamlı ölçüde daha büyük olduğunu gösterir.

iv. Varyans çözümlemede ilk olan bu makalede, Fisher (başka herkes tarafından öteden beri gözlenen gerçeği temsil ettiği kabul edilen) doğrusal modeli sorgulayarak düşüncesinin esnekliğini gösterdi. Yazarlar, “yukardaki sınama yönteme yalnızca bir örnek olarak verilmiştir; türler ve gübreleme işleminin etkilerini birleştiren toplama formülünün amaç için gayet uygunsuz olduğu bellidir. Kimse, yüksek verimli bir türün gerçekteki verim artışının aynısını düşük verimli bir türden beklememelidir….verimin, biri türe ve diğeri de gübreye bağlı iki faktörün çarpımı olduğu daha geçerli bir varsayımdır.” demektedirler[13, s.316]. Fisher’in hergünkü düşüncesinin bu kadarlık bir parçasının biçim değiştirmesine olanak vererek, şimdi onun bu yolda ilerleyeceğini bekleyebiliriz, ama gerçekte o, ancak son zamanlarda yeniden keşfedilen yöntemleri bularak, doğrusal olmayan uygun çözümlemeyi türetir[18]..⇑

Tarla deneyleri ile günlük çamurlu ilişki içinde olan birinin, normal dağılmış bağımsız hatalar gibi her hangi bir doğrudan varsayıma inanacağı pek beklenemez. Hataların marjinal normallik sayıltısı zararsız görülebilse de, arazinin bitişik parsellerindeki hataların bağımsızmış gibi işleme alınabileceğini öne sürmek açıkça anlamsız ve tehlikeli olabilir. Bu Fisher’in, (i) bir deneyin geçerliliği için gerekli bir koşul olarak fiziksel rassallaştırma işi üzerinde ve (ii) rassallaştıma yapıldıktan sonra çıkarımların; genellikle standart normal kuramın yeterli bir yaklaşma sağladığı, rassallaştırma dağılımından yapılması konusundaki ısrarının önemli bir nedenidir.

Standart doğrusal modelle yapılan olağan yokluk sınamalarının tam geçerliliğini sağlamak için, hata vektörü \({\bf{e}}\)’nin yoğunluk fonksiyonunun küresel normal olması elbette gerekmez, yalnızca küresel simetrik ⁵ , yani yoğunluk fonksiyonunun \(f({\bf{e’e}})\) biçiminde olması gerekir. Standart normal kuramın genellikle rassallaştırma kuramıyla verilene yeterli bir yaklaşma sağlıyor olması, rassallaştırılmış hatalara ilişkin yoğunluğun bağımsız normal ayrılışlarınki ile yaklaşılıyor olmasından dolayı değildir. Daha çok, uygun vektör uzayında rassallaştırma ile getirilen simetrinin küresel simetri ile yaklaşıklanıyor olmasındandır.

Çalışmasında yalnızca zengin bir matematiksel gelişme gören sonrakilere, biraz içerlemiştir. Özellikle, “dağılımdan bağımsız” sınama adı verilen konu üzerinde çalışanlar genellikle, ortak hata dağılımının simetrikliği gerekli varsayımının getirdiği sınırları vurgulamakta ve belki de kimi zaman farkına bile varmada başarısız olmuşlardır. Bu varsayımın geçerliliği, elbette ancak rassallaştırma ile sağlanabilirdi. Aksi durumda, türetilen yöntemler dağılımdan bağımsız olmak bir yana, hemen hemen normal bağımsız hatalar varsayımı üzerine türetilenler kadar kısıtlayıcı olurdu. Uzun süredir kullanılıyor olmanın, yoğunluk fonksiyonlarının \(p({\bf{y}}) = \prod\nolimits_i {f({y_i})} \), ya da en azından \(S\), \({\bf{y}}\)’nin elemanlarının simetrik bir fonksiyonu olmak üzere
\(p({\bf{y}}) = S({\bf{y}})\) biçiminde olduğu önermesini günahtan arındırmış göründüğü doğrudur. Bu önermeler neredeyse doğa yasaları ya da en azından hiçbir spor adamının sorgulayamayacağı oyunun kuralları gibi ele alınır olmuştur. ⁶ Gerçekte, hataların bağımsız olmasının beklenemeyeceği deneyler elbette çok yaygındır.

Bunlar yeni değildir, ancak Fisher’in bakış açısının hakkını vereceksek bir araya getirilmeleri ve birlikte gösterilmeleri gerekir. Bu sonraki amaç için, basit bir örnekleme deneyinin sonuçları çizelgede gösterilmiştir. Belirtilen biçimdeki özdeş yığınlardan

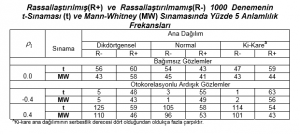10’ar gözlemlik iki örnek alınmış ve bir t-sınaması (t) ve bir Mann-Whitney sınaması (MW)’ndan geçirilmiştir. Örnekleme 1000 kez yinelenmiş ve yüzde 5 anlamlılık düzeyinde anlamlı bulunan sonuçların sayıları verilmiştir. İdeal olarak bu sayı 50 (yani, toplamın yüzde beşi) olmalıydı, ancak örnekleme hatalarından dolayı 7’ye yakın bir standart sapması bulunmaktadır. Daha büyük çaplı örnekler alınarak ya da analitik yöntemlerle daha doğru sonuçlar alınabilir, ancak örneğin yüzde 4’lük ve yüzde 6’lık anlamlılık düzeyleri arasında pratikte bir fark olmadığından, burada sunulan örnek yeterlidir.
\({y_t} = {u_t} – \theta .{u_{t – 1}}\) biçiminde bir hareketli ortalama modelinden gözlem üretilerek birbirine komşu değerlerler arasındaki otokorelasyonlar bulunmuştur. Bu modeldeki \(u_t\), çizelgede belirtilen biçimde sıfır etrafında birbirinden bağımsız ve özdeş dağılımlıdır. \(\theta\) değerleri, birinci dizisel korelasyon \(\rho_1\) değerleri, –0.4 ve +0.4 olacak biçimde seçilmiştir.

R- altında gösterilen frekanslar rassallaştırılmamış bir sınama için elde edilenlerdir. R+ altındakiler, gözlemler iki gruba rassal olarak dağıtıldığında bulunanlardır. Dağılımdan bağımsız sınamanın güvence sağladığı marjinal ana dağılımda yapılan esaslı değişikliklerden, t-sınamasının anlamlılık düzeyi beklendiği üzere dikkate değer ölçüde az etkilenmiştir. Ne yazık ki, hemen hemen aynı ölçüde başarılıyken rassallaştırma yapılmadıkça, elbette iki sınama da hata bağımlılığından dolayı aynı ölçüde bozulurlar. Elbette mesele, dağılımdan bağımsız sınama fonksiyonunun tanıtılması değil, burada asıl önemli olan rassallaştırma eylemidir..⇑

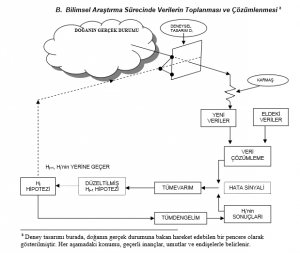
Eden’in patates verileri varyans çözümleme yöntemini göstermeye hizmet etti, ancak Fisher, o deneyin planlanma işine karışmış gözükmüyor. Tasarım ne rassallaştırılmış ne de bloklanmıştı, ve belirgin eksiklikleri uygun düzeltmeleri gerektiriyordu. Fisher’in dostu Gosset makaleyi görünce, “ Deney bana gayet kötü planlanmış görünüyor, ona bir el atmalısın…” diye yazdı. Fisher daha sonra, “ deney tasarımına başlaması gerektiğini öneren” Gosset’i dinler[15, 29.Mektup’un özeti]. Bunu yapmaya yönelir. Tasarım aşamasını içeren iterasyon süreci Şekil B’de kısaca tarif edilmiştir.

1919 ve 1928 arasında, kuram ve uygulamanın etkileşimi ile her birinin mantıksal olarak bir sonrakine yol açtığı üç ana aşamadan geçen bir dizi iterasyon oluştu. Varolan kayıtların çözümlenmesinden deneysel araştırma verilerinin çözümlenmesine, ve buradan da deneysel araştırmaların tasarımına geçildi.

Bu gelişmenin farklı ama etkileşimli aşamaları vardır. Bunlardan, (i) gelişen gereksinmelere karşılık bir dizi yeni yöntemin evrimini, (ii) uygulamacıları yeni teknikleri kullanmaya ikna etmeyi, ve (iii) gelişmenin gerektirdiği istatistikçinin değişen rolünü görebiliriz..⇑

3.12 Yeni Yöntemlerin Evrimi

Fisher’in deneysel verileri çözme girişimi, kendisini hemen deneysel tasarımın temel ilkelerine yöneltti. Geçerliliği sağlamak için rassallaştırma; hatanın geçerli bir tahminini elde etmek için, yineleme; doğruluğa ulaşmak için, karmaşın dışsal kaynaklarını bloklama gereksinimi. Aynı anda iki yönlü (rassallaştırılmış Latin karelerle) bloklama özellikle çekiciydi. Örneğin, oldukça dengesiz farklı biçimde gübreleme uygulanmış 13 Broadbalk parseline ilişkin farklılıklara anlam verme konusundaki ilk girişimler Fisher’i, bileşim içindeki değişkenlerin etkilerini değerlendirmenin kestirme bir yolu olarak, geleneksel olmayan faktöriyel düzenlemelerin büyük yararlarını görmeye yönlendirmiş olmalı. Ancak, faktöriyel tasarımların etkinliği daha fazla faktör bir araya getirilerek arttırılabilirse de, daha geniş faktoriyel tasarımlar daha büyük bloklar gerektirir ve bundan dolayı da daha büyük deneysel hata veren, deneysel malzemede daha fazla türdeş olmamayı doğurur. Hemen gelen yanıt, katıştırmadır..⇑

Onun tasarımları ancak uygulayıcılar tarafından denendiğinde geribeslemenin nimetleri elde edilebilirdi, fakat Fisher’in Rothamsted’deki devrimci düşüncelerinin hemen benimsenmesinin kolay bir iş olmadığına şaşmamak gerekir. Hatta, (1924’de) onun belirlediği doğrultudaki ilk tasarım uygulaması Rothamsted’de yapılmadı bile. Bu, onun öğütünü isteyen ve öğütü doğrultusunda giden Ormancılık Komisyonu için Bagshot’ta yürütülen rassallaştırılmış bir Latin Kare tasarımıydı. Ancak 1924 ile 1929 arasında, “Ürün Değişmesi Üzerine Çalışmalar IV ve VI” [5, 6] da anlatıldığı gibi, uygulamaya erken konan düşüncelerin hızlı bir gelişmesi görülür. Bu dönemde Eden’in inanmış bir yandaş olduğu açıktır, ama ne yazık ki yabancı kaldığı yeni tasarımların başarılı kullanımlarından elde edilen verilerle aynı anda yayınlandığını görmek güç veriyordu. Artık bu dönemin sonunda veriler, Fisher’in tüm düşüncelerini içeren çok duyarlı ve güzel tasarımlardan elde edilmektedir.

Tüm bunlara rağmen 1926’da Rothamsted Yöneticisi, Sir John Russell, koruması altında bulunan birinin düşüncelerini hemen tümüyle gözardı eden tarımsal deneyim hakkında Journal of the Ministry of Agriculture’da bir makale yazdı [16]. Ancak Fisher, patronuna doğruları koyan ve dinleyecek başka herkese, açık ve kısa oluşuyla dikkate değer bir makale ile bir sonraki sayıda [9], konu üzerindeki felsefesini özetledi..⇑

Araştırma istasyonunun istatistikçi gereksinmesi özgün kavramı devrimciydi, fakat 1919’da istatistikçi için başlangıçta uygun görülen rol elbette pasif ve hatta geçiciydi. Russell, mevcut kayıtlardan daha fazla her hangi bir şey çıkarılabilir mi diye merak etti.

Fisher’in çalışması giderek istatistikçinin işinin tüm iş bittikten sonra başlamadığını – iş başlamadan çok daha önce başladığını ortaya koydu. İstatistikçi, bir tozlu kutsal emanetler müzesi müdürü değildi. Onun bilimsel takıma karşı sorumluluğu, yeni tür bir deneyin araştırmasal yapısının güvenilir ve ucuz olmasını sağlayan bir mimarın can alıcı işi gibidir. Sonraki rolü öncekinden çok daha zevklidir. Kendisi ona tat vermiştir ve bize miras olarak bıraktığı için ona teşekkür etmemiz gerekir. O, yüksek düzeyde yetenekler ister. Diğer şeyler arasında, karmaşık bilimsel sorunları kavrayacak anlayış, dinleme sabrı, doğru soruları sorma feraseti, ve neyin önemli ve neyin önemsiz olduğunu görecek akıl gerektirir. Son olarak, bir deneyin her yürütülüşünde, istatistikçiden itibarını ortaya koyma cesaretini bekler. Tüm verilerin elde edildiği ve sonuçların çıkarılacağı an geldiği bu aşamada, tasarımda gözden kaçırılan bir şey varsa, şimdi ortaya çıkacak ve onu utandıracaktır..⇑

---

² Bu makale[8] Royal Society’ye genel başlıksız ancak garip biçimde III adı verilerek sunulmuş ve açıkca baştan bu dizi için düşünülmüştü.

³ İstatistiksel eleştiricilik yerinde adlandırması, Cuthbert Daniel’e aittir.

⁴ 1890,1891,1905,1906, ve 1915 olmak üzere beş yıl, bu yıllarda parsellere özel işlem uygulandığından ihmal edilmiştir.

⁵ Açıkça, verilerin sıfırıncı dereceden homojen bir fonksiyonu olan her hangi bir kıstas için bu doğru olmalıdır.

⁶ Zaman dizileri çalışmaları dışında.

Kuram ve uygulama arasındaki geribeslemenin bir sonucu olarak on yıllık kısa bir sürede bilimimizde yapılan olağanüstü ilerlemenin birkaç örneğini gördük. Geribesleme kapalı bir döngü gerektirir. Aksi durumda, her hangi bir nedenle döngü açık olduğunda, gelişme durur. Böyle bir tıkanma, ya uygulama ya da kuramda içine saplanılıp kalınan (normal olarak iteratif ) bir devirle oluşabilir..⇑

Ortaya çıkan hastalıklara kitapahçılığı ve matematikçilik denebilir. İlkinin belirtileri, araştırmanın gerçek amaçları ya da zoraki yöntemlerin gerektirdiği varsayımların ilintisi üzerinde yeterince düşünmeden, tüm sorunları bir veya iki alışılmış tekniğin kalıpları içine zorla sıkıştırma eğilimidir. Sonrakine ilişkin olarak, Fisher’in matematikçilere karşı açıkça ikili tutumu sık sık dile getirilmiş, şaşkınlık ve kızgınlık nedeni olmuştur. Matematiğin kullanımında bizzat kendisi bir sanatçıydı ve istatistikçiler için matematik eğitiminin önemini – daha fazla matematik bilmenin iyi bir istatistikçi olmak için daha fazla potansiyel demek olduğunu vurgulamıştır.Öyleyse kimi zaman matematikçilere neden öyle önem vermezmiş gibi göründü? Sanırım yanıt, onun asıl hedefinin “matematikçilik” olmasıydı. Burada ilk kez söylenen sözcüğün ayrımı yapılmalıdır.

Matematikçilik, uygulamaya nadiren yer verdiğinden, sorunları çözmek yerine onları yeniden tanımlama eğilimi olan, kuramın salt kuram için geliştirilmesi olarak tanımlanır. Tipik biçimde, uzun süre önce gözden kaybedilmiş, ancak bir zamanlar bilimsel bağlantısı olan istatistiksel bir problem vardır. Bu son noktayı, özellikle başlangıçta yararlı olan fikiri ürettiğinde, Fisher’in kendisi şiddetli biçimde hissetti. Deneylerin Tasarımı [11, s.48] kitabının III. Bölümü’nde tanıtılan düşünceleri yanlış kullandığını hissettiği dağılımdan bağımsız sınamalara değinmiştim. Canını sıkan bir başka şey de, kendi grup kuramı ve kombinatoriyal matematik uygulamalarının deneysel tasarıma genelleştirilmesiydi.

Bilimsel konunun dışında olmanın cezası, doğal olarak bilim topluluğunun istatistikçinin çalışmasını tanımamasıdır. Ancak bu toplulukla ilişkisi olmayan istatistikçinin bundan haberi bile olmaz. Bazen matematikçiliğin gerçek bir zararının olmadığı ileri sürülür. Bir zamanlar konuya ilişkin bir problemle oynayan ve asla yararlılığın tehlikeli sınamasından geçirilmeyen çözümler öneren bir grup kişi gayet mutlu tutulabilir. Toplantılarda birbirlerine makale okumaktan hoşlanırlar ve genellikle kimseyi incitmezler. Ancak, geçmişin bir döneminde iyi kullanılabilecekken boşa harcanan bu değerli yetenekler için elbette üzüntü duymalıyız.

Dahası, matematikçiliğin zararsız olmadığı yolunda pek de hoş olmayan kanıtlar vardır. Sosyoloji, psikoloji, eğitim, ve hatta üzülerek belirteyim ki, mühendislik gibi alanlarda, kendileri istatistikçi olmayan araştırmacılar kimi zaman matematikçiliği ciddiye almaktadırlar. Anlamadıklarıyla korkutulup kalmış olarak, yanlış biçimde kendi ortak duyularına güvenmezler ve bilimsel deneyimden yoksun matematikçiler tarafından geliştirilen uygun olmayan yöntemleri benimserler.

Matematikçiliğin çok daha ciddi bir sonucu da, istatistikçilerin eğitimine ilişkindir. Son zamanlarda, istatistikçiden pek fazla şey beklenmeyen bir dönemden geçmekteyiz. Büyük miktarda araştırma parasının bulunduğu ve istatistik öğretmeninin en büyük amacının bir başka istatistik öğretmeni olacak bir öğrenci yetiştirmek olduğu garip bir durum yaşandı. Böylece, ard arda konuyla ilgili herhangi bir uygulama bilgisi olmayan öğretmen nesilleri üretildi. Şimdi hemen her üniversitede istatistik bölümü bulunsa da, gerçek sorunlarla uğraşacak ciddi boyutta usta istatistikçi açığı sürmektedir. Ancak böylelerine gereksinim vardır..⇑

1950 gibi geçmiş bir tarihte, Cambridge’de Eddington Anısal Dersi’ni verirken Fisher,

Görebildiğimiz kadarı ile gelecekte, evrimleşen hemen her canlının çevresindeki ana etmeni insan ırkının eyleminin sağlıyacağı tartışmasız görülüyor. Bu gezegendeki yaratıcı eylemin ana yolları, ister bilinçli ister bilinçsiz biçimde insanın girişimi ve insanın seçimi olmuştur.Yeterince hazırlıklı olmadığımız, dünyanın verimli kaynakları üzerinde insanın hızla artan denetimi sonucu doğan ve tartışmasız bize düşen yeni sorumluluklar, ansızın olduğu gibi üzerimize yığılıp kalmıştır.

Dünyanın karşılaştığı çeşitli bunalımlar, birer birer, daha çok ortaya çıkmakta ve katı gerçekler için önlem alma gereksinimi kaçınılmaz olmaktadır. Dolayısı ile, verileri çözümleyerek, araştırmaları planlayarak, gerekli yeni kuram ve teknikleri geliştirerek gerçekleri didik didik edebilen usta istatistikçilere olan talep artmaya devam edecektir..⇑

Yetenekli istatistikçiler, yaşam savaşımızda ön cephe savaşcıları olacak-ancak onları nasıl bulacağız? İstediğimizin ne yalnızca teorem ispatlayıcılar, ne de yemek kitabı kullanıcıları olmadığında birleşmek için şimdi büyük bir istek olduğunu sanıyorum. Kuram ve uygulamanın tam bir dengesi gerekir. Ve en önemlisi, deneyim ve örnekle elde edilmek zorunda olan bir yeteneneği, nasıl iyi bir bilimci olabileceklerini, istatistikçiler öğrenmek zorundadırlar. Bir kez daha Fisher’in sözlerini aktaracak olursak, 1952’de İskoçya’da kurulması önerilen bir İstatistik Merkezi’ne ilişkin bir mektupta şöyle der: “Tartıştığınız böyle bir merkezin, keskin zekaların tümüyle verimsiz bir ortam içinde soyutlandığı iflas ettirici gidişin aksine, öğrenme yeteneği olanların uygulama deneyimi kazanabilecekleri proje çalışmaları ile yakın biçimde öğretimi birleştirmeyi planlamasını önermekten hiç çekinmem”[3]. Git gide daha çok istatistik merkezinde, bu öğütün şimdi ciddiye alınıyor olması umut vericidir..⇑

Fisher’in,

• Uygulamalı bir istatistikçi mi?
• Matematiksel bir istatistikçi mi?
• Bir veri çözümleyici mi?
• Bir araştırma tasarımcısı mı?

olduğunu sorabiliriz.

O bunların tümü olduğundan, kuşkusuz parçaların toplamından daha da fazlayısıydı. O, izleyebileceğimiz bir örnektir..⇑

[1] Box, G.E.P. and Tiao, G.C., Bayesian Inference in Statistical Analysis, Reading, Mass.: Addison- Wesley Publishing Co., 1973.

[2] _______ and Yule, P.V., “The exploration and Exploitation of Response Surfaces: An Example of the Link Between the Fitted Surfaces and the Basic Mechanism of the System,” Biometrics, 11, No.3 (1955), 287-323.

[3] Box, Joan Fisher, Fisher, The Life of a Scientist, New York: John Wiley & Sons, Inc. Baskıda.

[4] Cochran, W.G., “Experiments for Nonlinear Functions,” Journal of the American Statistical Association, 68, No.344 (1973),771-81.

[5] Eden,T. And Fisher, R.A., “Studies in Crop Variation IV. The Experimental Determination of the Value of Top Dressings with Cereals,” Journal of Agricultural Science, 17 (1927), 548-62.

[6] _________ and Fisher, R.A., “Studies in Crop Variation VI. Experiments on Response of Potato to Potash and Nitrogen,” ,” Journal of Agricultural Science, 19 (1929), 201-13.

[7] Fisher, R.A., “Studies in Crop Variation I. An Examination of the Yield of Dressed Grain from Broadbalk,” Journal of Agricultural Science, 11, (1921), 107-35.

[8] _________, “Studies in Crop Variation III. The Influence of Rainfall on the Yield of Wheat at Rothamsted,” Philosophical Transactions of the Royal Society of London, B, No. 213, (1924), 89-142.

[9] __________, “The Arrangement of Field Experiments,” Journal of the Ministry of Agriculture, 33, (1926), 503-13.

[10] _________, “Creative Aspects of Natural Law,” The Eddington Memorial Lecture, Cambridge, Eng.: Cambridge University Press, 1950.

[11] __________, The Design of Experiments, 8th Ed.), Edinburgh: Oliver & Boyd, Ltd., 1966.

[12] __________, Statistical Methods for Research Workers, (14th Ed.), Edinburgh: Oliver & Boyd, Ltd., 1970.

[13] _________ and MacKenzie, W.A., “Studies in Crop Variation II. The Manurial Response of Different Potato Varieties,” Journal of Agricultural Science, 13 (1923), 311-320.

[14] __________ and Tippett, L.H.C., “Limiting Forms of the Frequency Distribution of the Largest and Smallest Member of a Sample,” Proceeding of the Cambridge Philosophical Society, 24 (1929), 180-90.

[15] Gosset, W.S., Letters from W.S. Gosset to R.A.Fisher, 1915-1936, with summaries by R.A.Fisher and a foreword by L.McMullen, (2nd. Ed.), Özel olarak yayıldı, 1970.

[16] Russell, E. John, “Field Experiments: How They Are Made and What They Are,” Journal of the Ministry of Agriculture, 32, (1926), 989-1001.

[17] _________, A History of Agricultural Research in Great Britain, London: Allyn an Unwin, Ltd., 1966.

[18] Wold, H. “Nonlinear Estimation by Iterative Least Squares Procedures,” in F.N. David, ed., Research Papers in Statistics, Festschrift for J. Neyman, New York : John Wiley & Sons, Inc., 1966,411-44..⇑